ESTIU!!!

Ja estem a res de començar les vacances! Arriba l'estiu, la calor, la platja... i desde aquí al blog us desitjem molt bon estiu!!



Es l'hora de la diversió i de passar-ho bé, però sense oblidar les coses apresses aquest any i sobretot sense oblidar-nos de les matemàtiques. Aquí en el blog ens pendre'm una mica de descans del nostre blog, però espre'm tornar el curs que bé amb molta energia i les mateixes ganes que li possem sempre al nostre blog.
Gràcies als que ens heu seguit i heu après gràcies a nosaltres.

MARIONA CANET

Teorema de Varignon

Avui parlarem d'aquest famós teorema de Varignon
Primer començarem parlant del creador d'aquest teorema

Pierre Varignon

Pierre Varignon va néixer en una família de catòlics, era una família de paletes pobres i Pierre Varigon va dir que l'únic que havia rebut de la seva família era coneixement tèncic, que més tard li va ser molt valuós. Va estudiar al col·legi dels Jesuïtes a Caen on es va entrenar per ser sacerdot. En el 1676 va prendre les ordres sagrades i va ser admès en el sacerdoci. Més tard es va convertir en un sacerdot a la parròquia de Sant-Ouen, a Caen.
Però de cop la seva vida va cambiar de rumb quan es va trobar amb el llibre "d'Elements" d'Euclides i això va fer que s'interesses per les matemàtiques i es va dedicar a les ciències matemàtiques. Més tard es va traslladar a París on es va posar en contacte amb matemàtics i científics.
Més tard al 1687 va publicar la nova mecànica i es va convertir en professor de matemàtiques.

El teorema de Varignon és el seguent:
Si cada un dels costats AB, BC, CD i DA quadrilàter es divideix en parts iguals per els punts de divisió F, G, H i E i aquests punts són conectats per línies rectes FE, EH, HG i GF, el quadrilàter resultant és un paral·lelogram.

Què és un paral·lelogram?
Un paral·lelogram és un quadrilàter on els seus costats són oposats i paral·lels entre si, tenen la mateixa longitud i els angles oposats són iguals.
Els paral·lelograms són: cuadrat, rectangle, rombe i romboide

                                                                                              MARIONA,CANET I SOLER

El nombre auri

El nombre auri (també anomenat nombre d'or) és un nombre irracional, que en grec està representat com "phi". Aquest nombre va ser descobert a l'antiguitat i el podem trobar tant en formes geomètriques com a la natura.

El nombre auri en l'art

El nombre auri es pot trobar en moltes obres de Leonardo Da Vinci, a ell l'interesaven molt les matemàtiques a la natura i a l'art, l'home de Vitruvi conté aquest número i es por veure on cada part d'aquest cos tenen relació amb la secció àuria.

També podem veure que la Mona Lisa tanca un rectangle daurat perfecte

Però Leonardo no va ser l'únic que va utilitzar aquest número en les seves obres. Miguel Àngel va utilitzar el nombre auri en la seva escultura El David, desde la posició del melic amb respecte l'altura fins la colocació de les articulacions dels dits.

La primera persona a fer un estudi sobre aquest nombre va ser Euclides

Euclides va ser un famòs matemàtic de l'antiguitat, va ser educat a Atenes. Es deia que era fill de Naucrates, i la seva obra més famosa va ser "Elements". La geometria d'Euclides ha sigut útil per a la física, astronomia, química i matemàtiques.

En la seva obra Euclides va definir el valor del nombre auri dient que: una línia recta està dividida en l'extrem i el seu proporcional que la línia sencera és al segment major com el major és el menor. És a dir: dos nombres positius a i b estan en raó àuria si (a + b)/ a = a/ b.
El valor aproximat d'aquest nombre és és 1,6180339887498...

Aquest nombre també està relacionat amb la succeció de Fibonacci (que ja vem parlar més enrere en el nostre blog)

MARIONA,CANET I SOLER

MATEMÀTIQUES AMB REFRANYS

Volguem o no, les matemàtiques ens envolten dia dia, i no només Per el que fem, sinó a l’hora de parlar. Diem refranys o frases que acaben tenint una relació matemática:

“Cada dos per tres”

Vol dir que sovint fa algo.

“A la tercera va la vençuda"

Significa que després de molts intents,surt.

“Sóc un cero a l’esquerra”

Quan una persona es sent inferior.

“Mes val sumar que restar”

Mes val tenir que perdre.

“Anem a cero”

Quan vas a per totes amb ganes d'obtenir-ho tot.

“Vaya par de dos”

Vaya parelleta de bons nens.

“No sempre dos mes dos són quatre”

Avegades reps menys del que et pensabes.

Com podeu veure totes aquestes frases o refranys estan plens de matemàtiques sense donar-nos compte, així la gent es dona compte de que les matemàtiques ens envolten.

Elena González

Tales de Mileto

PRIMER TEOREMA:

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.

De hecho el primer teorema de tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo.                                        

        

                         

                                 Por ejemplo en la figura se observan dos triángulos que, en virtud del teorema de Tales son semejantes , entre los lados A y B del triangulo pequeño es el mismo que el cociente entre los lados D y C en el triangulo grande.

SEGUNDO TEOREMA:

Sea B un punto de la circunferencia de diámetro AC y centro "O", distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo donde <ABC = 90º.

1r vidio explicación ( por si de caso )

2nd una canción 

Les matemàtiques a l'antiguetat

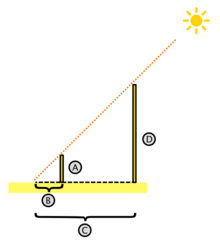
A l'ultima entrada vem estar parlant d'un matemàtic grec, i m'ha semblat oportú parlar una mica sobre les matemàtiques temps enrere.

Al principi les matemàtiques eren considerades ciències de quantitat, apartir del segle XIX es van començar a considerar les ciències de les relacions.

Les matemàtiques a l'antiguetat

Les primeres referències sobre les matemàtiques començen a Babilonia i Egipte



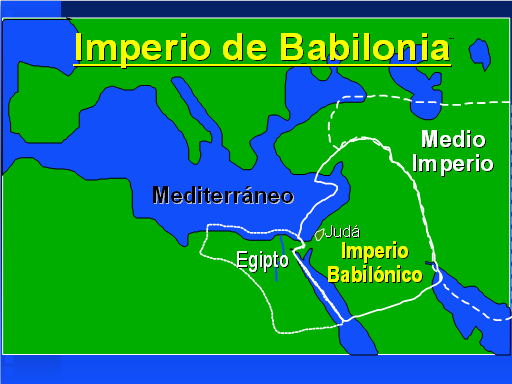
En aquella època els números es representaven escribint el símbol del 1 tantes vegades com unitats tenia el número que volien representar. Utilitzaven el símbol del 10 per representar tantes desenes com tenia aquell número. I per sumer números es sumaven per separat les unitats, desenes i centenes de cada número.

Les matemàtiques aplicades a Grècia

Els grecs van agafar elements matemàtics dels egipcis i els babilonis. La innovació més important va ser inventar matemàtiques basades en una estructura lògica de definicions, demostracions... es va començar al segle VI a.c amb Tales i pitàgores.
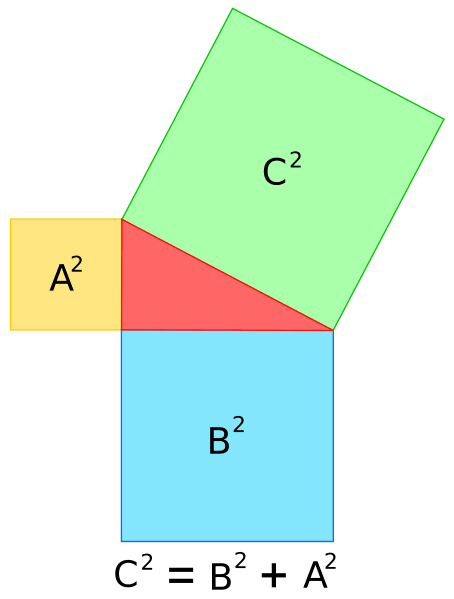
El teorema de Pitàgores diu que en un triangle rectangle, el quadrat de la hipotenusa és a dir el que és més llarg, és igual a la suma del quadrats de les cares més petites del triangle que fan l'angle recte.



Àntic Orient Pròxim

Aquestes matemàtiques eren les matemàtiques de la gent de mesopotàmia. Es diu babilonia per el lloc d'estudi on temps més endavant va desaparèixer.
Es van barrejar les matemàtiques babilòniques amb les matemàtiques gregues i egipcies i es va anomenar: matemàtiques hel·lenístiques.

Egipte

Les matemàtiques egipcies són les matemàtiques escrites en llengua egípcia. El text matemàtic més antic va ser el papir de Moscú, que és del Imperi Mitjà d'egipte 2000- 1800 a.c. Són problemes amb pareules i un és el mètode per trobar el volum d'un tronc.



MARIONA CANET I SOLER

Avui us volem parlar d'un matemàtic Grec anomenat
Euclides

 
Euclides va ser un dels matemàtics més famosos de l'antigüetat grega i molt conegut a la història de les matemàtiques. No es coneix molt sobre la seva vida, però sí sobre la seva famosa obra.
Se sap que vivia a Alejandria cap el 300 a.c. i va crear una escola matemàtica.

La seva gran obra es diu "ELS ELEMENTS"
Amb aquesta obra es demostra que aquest matemàtic va ser el més llegit de la història, ja que el seu llibre va tenir més de 1.000 edicions.
Els 5 famosos postulats (demostracions bàsiques per entendre coses més complicades) de Euclides són:

1- Amb dos punts es pot fer una línia que els uneixi



2- Qualsevol segment pot ser allargat de forma contínua i ilimitada en la mateixa direcció.


3- Es pot fer una circumferència agafant qualsevol punt i radi



4- Tots els angles rectes són iguals.


5- Si tenim una recta i la tallem amb dues més es formaran dos angles més petits a un angle de 90 graus, i si les dues rectes les estirem indefinidament es tallen del costat on estan els angles menors


MARIONA CANET I ELENA GONZÀLEZ

BON DIA ESTIMATS SEGUIDORS!!!

Ara us explicarem els nostres objectius amb aquest blog fins a final de curs.
Objectius amb grup:

- Millorar la qualitat de les entrades en aquest blog.
- Treballar en grup
- Informar-nos més de les coses que publiquem

Objectius personals 

Objectius Elena:

-Poguer cada cop millorar més el nostre blog i aconseguir que a la gent li agradi.
-Intentar fer veure a la gent que les matemàtiques són essencials en la vida i que estem envoltats d'elles.
-Mentres busco informació per al blog poguer anant aprenent jo també.

Objectius Mariona:
- Informar-me molt bé de tot el que poso en cada publicació.
- Que la qualitat de les meves publicacions cada vegada siguin millors.
- Que després de cada publicació no només estigui donant informació als demés, sinó que també aprengui jo de cada publicació.

MARIONA CANET I ELENA GONZÁLEZ